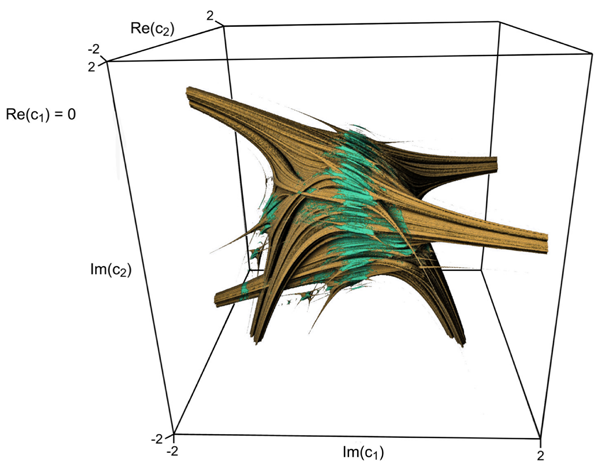
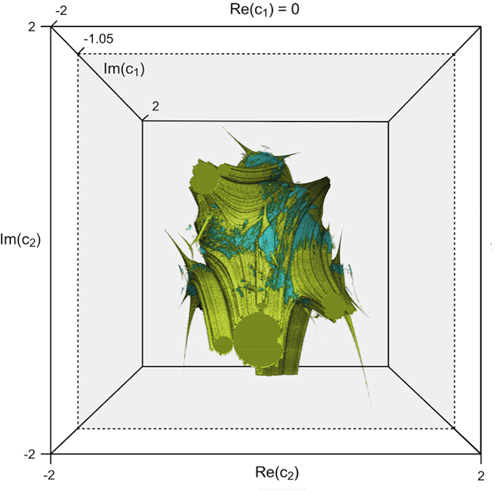
RIST’s scientist Marius F. Danca and his colleagues have discovered, using experimental mathematics aided by leading edge computer graphics algorithms, that the Mandelbrot set is not only, as known, the set of all complex points for which the Julia sets are connected, but also the set of all points for which the alternated Julia sets are disconnected. The results have been published in the Nonlinear Dynamics journal. Alternated Julia sets have been also introduced by Marius F. Danca, in 2009.
The connectivity sets of alternated Julia sets form a four-dimensional body. The scientists have shown that there are two-dimensional slices through this body where the set of all parameter values for which each corresponding alternated Julia set is disconnected is the Mandelbrot set or, at least, resembling the Mandelbrot set.
References:
Marius-F. Danca, Paul Bourke, Miguel Romera (2013), Graphical exploration of the connectivity sets of alternated Julia sets: M, the set of disconnected alternated Julia sets, Nonlinear Dynamics, http://dx.doi.org/10.1007/s11071-013-0859-y
Marius-F. Danca (2009), Alternated Julia sets and connectivity properties, International Journal of Bifurcation and Chaos 19 (6), pp. 2123-2129, http://dx.doi.org/10.1142/S0218127409023962