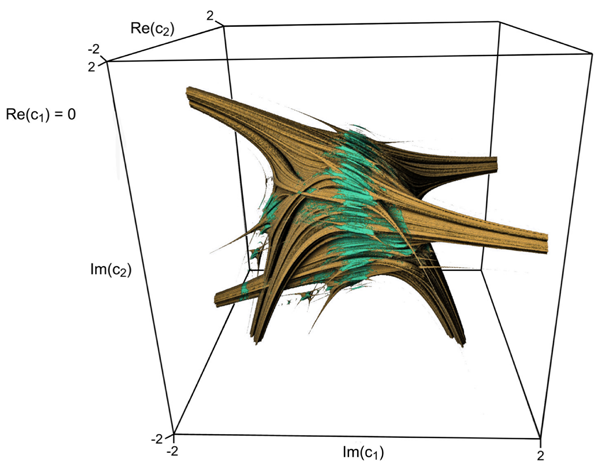
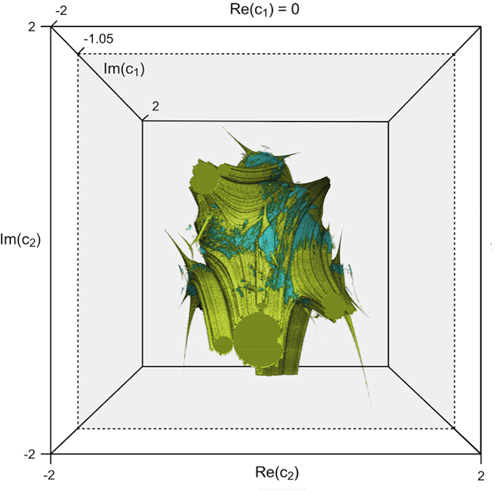
Marius-F. Danca, cercetător afiliat institutului nostru, şi colaboratorii săi au descoperit cu ajutorul matematicii experimentale, ajutaţi de algoritmi performanţi de grafică computaţională, faptul că mulţimea Mandelbrot este nu numai mulţimea tuturor punctelor din planul complex pentru care mulţimile Julia sunt conexe, dar şi mulţimea punctelor pentru care mulţimile Julia alternate sunt neconexe. Aceste rezultate au fost publicate în revista Nonlinear Dynamics. Mulţimile Julia alternate au fost introduse tot de Marius-F. Danca, în anul 2009. Mulţimile de conectivitate pentru mulţimile Julia alternate formează un corp cu 4 dimensiuni. In lucrarea menţionată, autorii au dedus că există secţiuni bidimensionale prin acest corp, în care mulţimea tuturor valorilor parametrilor pentru care mulţimile Julia alternate sunt neconexe formează mulţimea Mandelbrot.
Referinţe:
Marius-F. Danca, Paul Bourke, Miguel Romera (2013), Graphical exploration of the connectivity sets of alternated Julia sets: M, the set of disconnected alternated Julia sets, Nonlinear Dynamics, http://dx.doi.org/10.1007/s11071-013-0859-y
Marius-F. Danca (2009), Alternated Julia sets and connectivity properties, International Journal of Bifurcation and Chaos 19 (6), pp. 2123-2129, http://dx.doi.org/10.1142/S0218127409023962